1.電磁界解析とは/ノイズ解析とは
電磁界解析とは、端的に述べれば「電磁界解析法を使ったシミュレーション」である。詳細は後述するが、時間領域法(有限差分領域法:FDTD、伝送線路法:TLM)での解析と、周波数領域法(有限要素法:FEM、モーメント法:MOM)、その他には等価定数回路網法も存在する。基本的にはシミュレータを使ったEMC解析である。
電子情報機器の高速化、および製品サイクルの短期化等により、回路、基板、筐体等の設計の段階から、EMCフリーな性能を確保する必要が出てきており、そのような電子情報機器のEMCを計算機上で検討するシミュレータ( 電磁界解析ソフト・EMCシミュレータ)を導入、利用するケースが増えてきている。
EMCの現象はマックスウェルの方程式で記述することが可能であるが、プリント配線板などの複雑な電気的構造物からの放射エミッション(EMI問題)を解析的に解くことは、ほとんどの場合困難である。
EMIシミュレーションの精度は対象構造物の電流分布をどれだけ正確に求めるかに依存する。
例えば、解析対象の構造物上での電流分布が一様であるとの電磁気的な仮定を導入した簡易型のシミュレータ(電磁界解析ソフト・EMCシミュレータ)では、周波数が低く(波長が長く)、対象構造物の電気長が十分に長い時を除いて、実際との間に差異を生じる。
2.電磁界解析/ノイズ解析の主な計算手法・方法(モーメント法/有限要素法/有限差分時間領域法)
最近では電磁界解析/ノイズ解析として多数の物が開発されている。
そこで使われる計算法は次の3つに大別される。
- ① MoM(Method of Moments):モーメント法
- 電磁界解析/ノイズ解析の手法の一つであるMoM法(モーメント法)は束縛の無い放射問題のEMC解析に非常に有効である。
完全導体で、一様な誘電物質からなる構造のEMC解析に優れているが、複雑な不均一な構造の解析には適さない。
- ② FEM(Finite Elements Method):有限要素法
- FEM法(有限要素法)は、表面だけをメッシュする表面積分法とは異なり、解析構造の全面積をメッシュする。一般に完全に不均質構造のモデリングに適しているが、モーメント法ほど効果的に放射問題をモデル化できない。
- ③ FDTD(Finite Difference Time Domain):有限差分領域法
- FDTD法(有限差分時間領域法)は、全空間のメッシュが必要である。
モーメント法や有限要素法と違って、FDTD法は時間領域での解析であるので、過渡解析に適している。
また複雑な不均質構造のモデリングに非常に優れている。
電磁界解析/ノイズ解析により、PCBの中にあらわれる種々の基本、あるいは補助的構造のEMC的振る舞いを明らかにすることが可能である。ただし、電磁界解析/ノイズ解析は実験を不要とするものではない。
しかしながら、実験からのみでは事実の把握が困難な場合も多々ある。
シミュレーションの持つ特質を生かすことにより、 EMCを対策問題から、設計問題へと移行させる手段として、EMCルールチェッカ等を含む、広い意味での電磁界解析(ノイズ解析)が今後の情報処理製品開発において重要になる。
<CENDおすすめ製品>
 【電磁界解析シミュレータ】
【電磁界解析シミュレータ】
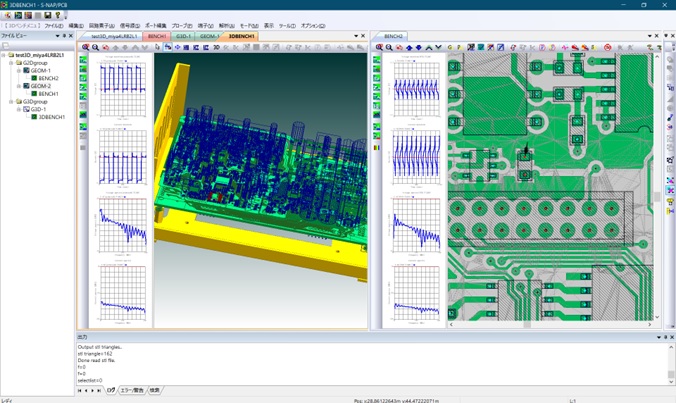
S-NAP/PCB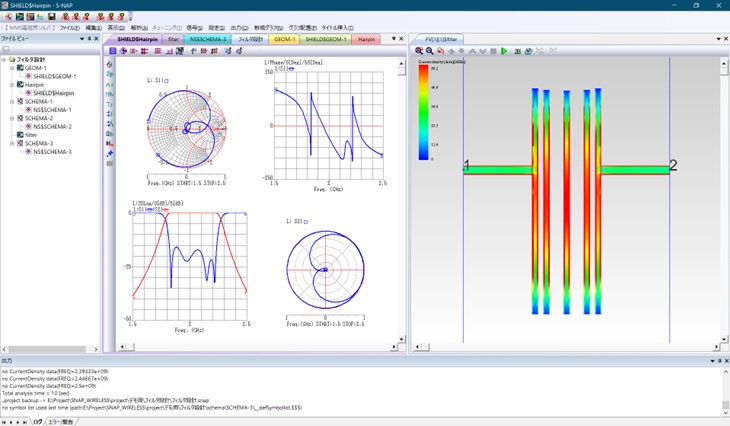 【電磁界解析シミュレータ】
【電磁界解析シミュレータ】
S-NAP/Wireless 【電磁界解析シミュレータ】
【電磁界解析シミュレータ】
EMCoS Studio 【電磁界解析シミュレータ】
【電磁界解析シミュレータ】
Altair Feko
3.電磁界解析/ノイズ解析のモデリング
電磁界解析/ノイズ解析におけるモデリングツールは、一つの計測器として考えればわかりやすい。
例えば、モーメント法を用いたツールでは、その精度とそれを与える条件は決まっているから、計測器を用いると同じように対象構造物をどのようにすれば必要な条件で計測できるかに注力すればよい。
実際の計測においてプロービングによる誤差などが生じるように、EMC解析においても実際の構造物とモデルの間の相違に伴ういわゆる誤差が生じうる。
ここがシミュレーションにおいて、技術力が発揮される領域となる。実際の計測では、計測の誤差、設計の誤差等を含めて実際の計測値が得られることになる。従って、計測結果に基づき、どのような誤差が含まれたのかを考慮しつつ、物理的挙動を調べることになる。
シミュレーションでは、計測で与えられるような誤差は生じない。
しかしながら、実際の計測値との間の差異を調べ、物理的挙動を調べる。
結果をもって、物理的考察をするということについては、両者は同じ位置付けであり、電磁界解析/ノイズ解析ツールを「計測器のようなもの」とする所以である。

 CEND.jp
CEND.jp
